در دنیای امروز، امنیت شبکه یک بحث چالش برانگیز است. تکنیک‌های زیادی برای تأمین امنیت و جلوگیری از حملات طراحی شده‎اند. میلیون‎ها نفر در سراسر دنیا به شبکه متصل بوده و هدف اصلی تکنیک‎های امنیتی، حفظ امنیت دیتا تا زمان رسیدن به مقصد می‎باشد. امنیت شبکه از پارامترهای محرمانه بودن، یکپارچه بودن و قابل دسترس بودن، کنترل دسترسی، ارائه مجوز و عدم انکار، اطمینان حاصل می‌کند. در این مقاله قصد داریم تا به نقش و اهمیت الگوریتم RSA در امنیت شبکه بپردازیم.

نقش الگوریتم RSA در امنیت شکبه

کریپتوگرافی، یکی از بهترین راهکارها برای برقراری ارتباط در شبکه است. کریپتوگرافی یک عبارت یونانی است که به معنی پنهان کردن اطلاعات می‌باشد. کریپتوگرافی از محرمانه بودن پیام، اطمینان حاصل کرده و درواقع یک دستورالعمل برای انتقال امن اطلاعات می‌باشد. براساس این دستورالعمل، اطلاعات به شکل رمزنگاری شده، همراه با کلید رمزنگاری و یا بدون کلید رمزنگاری، وجود دارد. پیام مورد نظر با یک الگوریتم و یک کلید از سمت فرستنده، رمزنگاری می‌شود و متن رمزنگاری شده که به عنوان متن محرمانه شناخته می‌شود، به سمت گیرنده ارسال شده و در آنجا، این متن با یک کلید توسط گیرنده رمزگشایی شده و پیام اصلی در آن قسمت به دست خواهد آمد.

الگوریتم RSA در امنیت شبکه نقش مهمی دارد و سرویس امنیتی را برای هر کاربری که به شبکه وصل است، فراهم می‌آورد. بسیاری از الگوریتم‌های کریپتوگرافی برای تبادل اطلاعات در سطح شبکه استفاده می‌شوند. الگوریتم کریپتوسیستم نیز یک الگوریتم کریپتوگرافی است که در مبحث امنیت شبکه، کاربرد گسترده‌ای دارد، اما این الگوریتم برای اعداد کوچک، مشکل تجزیه و فاکتورسازی اعداد طبیعی را دارد. محققان روش‌های اصلاحی زیادی را برای بهبود امنیت الگوریتم RSA ساده، پیشنهاد داده‌اند. در این پروژه تحقیقاتی، روش‌های اصلاحی گوناگونی ارائه شده و برای درک بهتر رویکردهای جدید کریپتوسیستم RSA، با هم مقایسه شده‌اند. تمام این رویکردهای جدید کریپتوسیستم RSA، سعی در بهبود امنیت داشته و زمان پروسه تولید کلید رمزنگاری و رمزگشایی را افزایش می‌دهند.

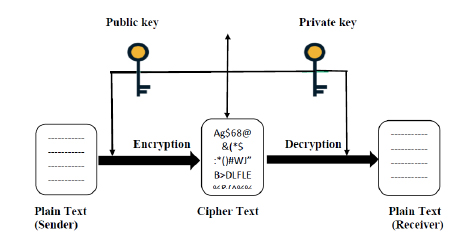
شکل 1. مدل کریپتوگرافی با کلید عمومی

کریپتوگرافی با کلید متقارن و کلید نامتقارن، هر دو مبتنی بر یک کلید عمومی و یک کلید خصوصی هستند. در کریپتوگرافی با کلید متقارن، تنها یک کلید یعنی همان کلید عمومی برای رمزنگاری در سمت فرستنده و رمزگشایی در سمت گیرنده استفاده می‌شود، بنابراین به راحتی توسط دیگران قابل دسترسی خواهد بود، این امر بدین معنی است که این روش برای انتقال دیتا، امن نیست. DES، AES، IDEA، Blowfish همگی از انواع کریپتوگرافی با کلید متقارن هستند. در کریپتوگرافی با کلید نامتقارن، دو کلید استفاده می‌شود، یعنی کلید عمومی و کلید خصوصی. در این روش، دیتای مورد نظر با استفاده از کلید عمومی در سمت فرستنده رمزنگاری شده و با استفاده از کلید خصوصی در سمت گیرنده، رمزگشایی می‌شود. بنابراین، این روش برای انتقال دیتا، امنیت بیشتری دارد، چرا که کلیدهای مختلفی برای رمزنگاری و رمزگشایی استفاده می‌شود. الگوریتم‌های RSA در امنیت شبکه از انواع کریپتوگرافی با کلید نامتقارن می‌باشد.

سیستم رمزنگاری RSA در امنيت شبكه

الگوریتم RSA در امنیت شبکه یکی از معروف‌ترین الگوریتم‌های کریپتوگرافی می‌باشد. این الگوریتم توسط Ron Rivest، Adi Shamir و Leonard Adleman در سال 1977 در دانشگاه MIT ابداع شده است. الگوریتم RSAدر امنیت شبکه کاربردهای گسترده‌ای دارد. در این الگوریتم، دو مسئله وجود دارد، مسئله اول، تجزیه اعداد طبیعی و مسئله دوم، پیدا کردن ریشه N ام. کاراکتر N درواقع حاصل دو عدد اول است. RSA از دو کلید عمومی و خصوصی استفاده می‌کند. کلید عمومی برای رمزنگاری و کلید خصوصی برای رمزگشایی استفاده می‌شود. براساس تئوری اعداد، محاسبه حاصل دو عدد بزرگ راحت است، اما تجزیه و فاکتورگیری از آن، سخت است. در الگوریتم RSA، امنیت به فاکتور اعداد بزرگ بستگی دارد. ابعاد کلید در الگوریتم RSA از 2048 تا 4096 می‌باشد که فاکتورگیری از آن خیلی مشکل است. رمزگشایی در الگوریتم RSA مبتنی بر d و N است. d نشان دهنده کلید رمزگشایی بوده و N هم نشان دهنده عدد طبیعی است. پیچیدگی زمانی RSA نیز 0 (n2) می باشد. بهبود الگوریتم ‍RSA در امنیت شبکه از موضوعات اساسی است و اصلاحات زیادی توسط محققان برای بهبود الگوریتم RSA پیشنهاد شده است.

پروسه‌های ‍RSA در امنیت شبکه

سه پروسه در الگوریتم RSA وجود دارد، در ادامه به تشریح این سه مورد خواهیم پرداخت:

تولید کلید

تولید کلید طی مراحل زیر انجام می‌شود:

-تولید دو عدد اول بزرگ p و q به طوریکه عضو مجموعه gcd باشد (p,q)=1 .

-محاسبه n = p*q

-محاسبه تابع فی اویلر Ø(n) = (p-1)*(q-1) .

-انتخاب عدد صحیح کلید عمومی e به طوریکه در آن، 1 < e < Ø(n) € gcd (Ø(n),e) = 1 .

-محاسبه عدد صحیح کلید خصوصی d، به طوریکه d = e-1,mod Ø(n) .

-کلید عمومی برابر است با (e,n) و کلید خصوصی برابر است با (d,n).

رمزنگاری

رمزنگاری طی مراحل زیر انجام می‌شود:

-کلید عمومی (e,n)، متن محرمانه یا همان c و پیام خام و اصلی یا همان m

-رمزنگاری پیام در متن محرمانه c = me mod n

-A، متن محرمانه c را به B می‌فرستد.

رمزگشایی

رمزگشایی طی مراحل زیر انجام می‌شود:

-کلید خصوصی (d,n) .

-رمزگشایی متن محرمانه m = cd mod n

-B می‌تواند پیام اصلی را بخواند

تجزیه و تحلیل زمان صرف شده در الگوریتم

در این مقاله، ما نتایج الگوریتم‌های گوناگون را در اینجا با استفاده از python ارائه کردیم تا زمان صرف شده توسط الگوریتم‌های مختلف، مقایسه شود. به ازای c، ما از ماژول 16 بیتی ابعاد پیام 16 بیتی استفاده می‌کنیم.

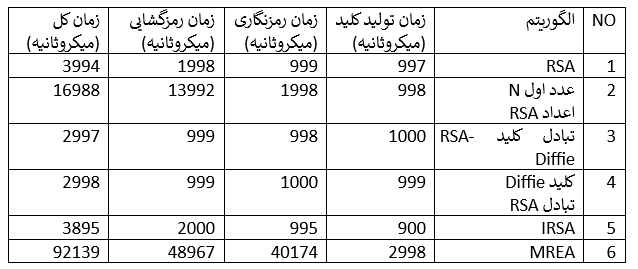
جدول 1. جدول مقایسه الگوریتم‌ها

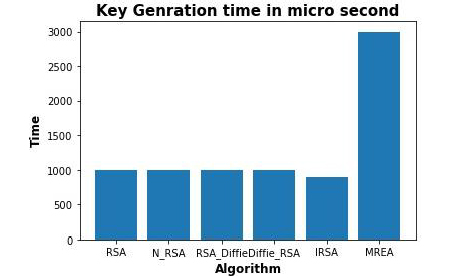
شکل 2. مقایسه زمان تولید کلید در الگوریتم‌های مختلف

شکل 3. مقایسه زمان رمزنگاری در الگوریتم‌های مختلف

شکل 4. مقایسه زمان رمزگشایی در الگوریتم‌های مختلف

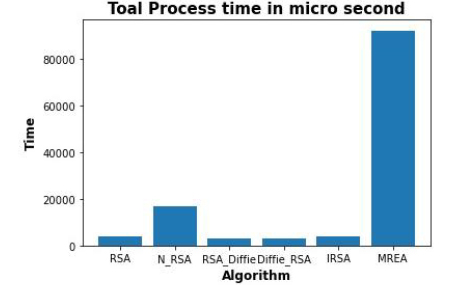
شکل 5. مقایسه زمان کل در الگوریتم‌های مختلف

نتیجه‌گیری

در این مقاله، برخی از روش‌های اصلاح الگوریتم RSA در امنیت شبکه تشریح شده است و محققان سعی بر این داشته‌اند که الگوریتم RSA امن‌تری را، توسعه دهند.

در مطالعات الگوریتم RSA عادی، سوالی که مطرح می‌شود این است که آیا این الگوریتم امن است یا خیر؟ امروزه کامپیوترها با پردازنده‌های بسیار قوی و سرعت اجرای عملکرد بسیار بالا در دسترس هستند. کامپیوتر کوانتمی یکی از این موارد است که قدرت پردازش بالای آن به سادگی می‌تواند هزاران بیت را پردازش کند. مطابق با فرضیه Riemann، اگر تناوب عدد اول پیدا شود، پیدا کردن فاکتور اعداد اول ضرب‌پذیر ساده خواهد بود. بنابراین یک الگوریتم RSA امن‌تر، مورد نیاز است.